The engineering team of RainforestQA (YC S12) is remote and distributed around the globe, with developers in America, Europe, and Asia. We’re using PagerDuty to assign developers on-call and for contacting/escalating people in case of incidents.
Our working hours cover almost all time-zones, about 22 hours from full time-zone coverage. Yet for distributing our on-call schedule, we were unhappy with PagerDuty’s standard daily rotation. For a distributed team, why does somebody need to be on-call at night when other team members are working right now?
Follow the sun scheduling from PagerDuty which is their solution for distributed teams didn’t work for us because it assumes you can group people by blocks of time that don’t overlap. This didn’t work for us because we have many people with many different working times.
The Tyrant
In 2017 we started an internal project called Tyrant to automatically solve this problem of fairly managing on-call scheduling across time-zones.
Originally the project was developed in Ruby with a few for loops and a bunch of if statements. But it didn’t distribute on-call time fairly, it was hard to update the algorithm, and it wasn’t flexible enough. Also, we were interested in applying discrete optimization in production for much harder problems and so we decided to start deploying discrete optimization to our on-call scheduling problem first so we could learn more.
Finally, in 2019 during a hackathon session in Kuala Lumpur we created the latest version of Tyrant which used discrete optimization.
Tyrant runs as a cron job every Saturday. It gets the working hour preferences of the developers, builds the on-call schedules, pushes them to PagerDuty, then emails the schedule to everyone.
This blog post is an introduction to discrete optimization for building the kind of on-call schedule we needed.

What is Discrete Optimization
Discrete optimization is the selection of a best element (answer) with regard to some criterion, and where some of the variables are restricted to be discrete (the number of permitted values is either finite or countably infinite).
I had used discrete optimization in hobby projects and for programming challenges. But for a long time I couldn’t find a use case at work; every time I had a project that was solvable through discrete optimization the naive algorithms were better because they got a good enough result faster and without the complexity of adding a discrete optimization system.
Tyrant is a completely different story. As it creates the schedule only once per week, speed isn’t important – the quality of the result is.
Tyrant’s core is implemented in MiniZinc. MiniZinc is a high-level modelling language and compiler. MiniZinc compiles into FlatZinc, a low-level language that is understood by a wide range of discrete optimization solvers. For us it means faster development, self-explanatory model, and ability to switch solvers.
Introduction to MiniZinc
Let’s explore a simple problem to familiarize ourselves with the basic MiniZinc syntax. Imagine you run a small car factory named “miniTesla”. You have 100 lithium batteries, and 190000 kilograms of metal. Building a “Cybertruck” requires 1 battery and 2500 kg of metal, while building “Model3” requires also 1 battery but only 1500 kg of metal. If you can sell a “Cybertruck” for $40k and “Model3” for $35k you’d like to know how many of each vehicle to produce to maximize your profits.
profit is our objective. It’s the variable in our case (or could be expression) which we’re trying maximize or minimize.
int: total_nb_battery = 100; % fixed input parameter
int: total_kg_metal = 190000; % fixed input parameter
% variable, possible number of different cars
var 0..total_nb_battery: nb_cybertruck;
var 0..total_nb_battery: nb_model3;
var int: profit = nb_cybertruck * 40000 + nb_model3 * 35000;
% limit total number of kilograms
constraint nb_cybertruck * 2500 + nb_model3 * 1500 <= total_kg_metal;
% limit total number of batteries
constraint nb_cybertruck + nb_model3 <= total_nb_battery;
% Find the value of the variables that makes the most money!
solve maximize profit;miniTesla example in MiniZinc playground
The amount of words to describe the problem in English would be about the same as in MiniZinc. The code is self-explanatory even without knowing a lot about the syntax.
There’s a few nuances:
int(first 2 lines) fixed integer variables – value should be definedvar intunfixed integer variable – MiniZinc figures out the value laterconstraintsome expression that should be true
The line: var 0..total_nb_battery: nb_model3; says variable nb_model3 should be an integer from 0 to total_nb_battery. This could be written as:
var int: nb_model3;
constraint nb_model3 >= 0;
constraint nb_model3 <= total_nb_battery;The last line solve maximize profit tells MiniZinc what to optimize.
If you have minizinc installed locally, you can solve the model with the command minizinc minitesla.mzn --output-objective and it should tell you how many cars to build in order to reach the maximized profit of $3.7M:
nb_cybertruck = 40;
nb_model3 = 60;
_objective = 3700000;
----------
==========--- means it found a solution, === means it found the optimal solution.
With a data file
To reuse the model we can split it into 2 separate files: a file for the model and a file for the data. In the model file we have variable definition without values like this:
int: total_nb_battery;
int: total_kg_metal;And the data file minitesla.dzn gives values for the model variables:
total_nb_battery = 100;
total_kg_metal = 190000;Command to run model with the separate data file: minizinc minitesla.mzn minitesla.dzn (BTW, the file extension is matters to MiniZinc – don’t change it!)
Source code of hello world with data file
Building our first on-call schedule model
Now we’re prepared to build our first simple on-call scheduling model. For input, the model takes developers preferences (does developer X want to be on-call at hour Y). The output: assign a developer to every hour next week. The final assignment should follow only one constraint: assign a developer to an hour according to their preferences.
Data Structures of scheduling model
Niklaus Wirth wrote the famous book Algorithms + Data Structures = Programs. For discrete optimization modeling, MiniZinc does Algorithms for us, so we only need to worry about the Data Structures part. For this problem we have 2 core data structures to define: the Input and the Output.
For output we use an array assignment which records which developer is on-call for every hour in the week and so has a size of 168 elements (because there are 7 days × 24 hours in a week).
int: nb_developers;
set of int: HOURS = 1..168;
set of int: DEVELOPERS = 1..nb_developers;
array[HOURS] of var DEVELOPERS: assignment;Besides array, we’ve introduced set of int which is an enumeration of the numbers from start to end inclusive. MiniZinc arrays have named indexes. In our example assignment has named indexes based on the range HOURS (1..168). The statement array[HOURS] of var DEVELOPERS: assignment = [7, 8, 9, …] therefore means developer 7 will be on-call at hour 1 (the first index of HOURS range).
We’ll make the input data a multi-dimensional array, with size DEVELOPERS × HOURS. This represents the mapping of developer and an hour to an integer in the set { 0, 1 }. Where a 1 means a developer is available for on-call.
array[DEVELOPERS, HOURS] of 0..1: working_hours;Example of a data file (notice how rows separated with | symbol):
nb_developers = 3;
working_hours = [|
0, 0, 1, ..., 0 |
0, 1, 1, ..., 0 |
1, 0, 0, ..., 1 |];One note about nb_developers. Theoretically we could get the value of nb_developers from working_hours, but in practice it’s a chicken and egg problem and MiniZinc has to be told nb_developers to enumerate properly over working_hours array.
Constraint and objective
We’re going to add our first constraint now: if a developer is not available at some hour in working_hours array, then we should not assign them to be on-call.
constraint forall(hour in HOURS, developer in DEVELOPERS)(
working_hours[developer, hour] = 0 -> assignment[hour] != developer
);-> means implication. For me it was easier to understand by thinking it as being equivalent to this pseudocode:
if working_hours[developer, hour] == 0:
add_constraint(assignment[hour] != developer)Unlike the miniTesla example, here we don’t need optimization, as we don’t have an expression to optimize. Instead, we simply ask MiniZinc to satisfy all the constraints:
solve satisfy;If you run it then a solution will be available in a few milliseconds.
assignment = array1d(1..168, [1, 1, 1, ..., 1]);
----------The solution says it’s not so much fun to be the first developer.
First unfair model in MiniZinc Playground or on GitHub
Fairness
Let’s add fairness to the model. We’re going to define fairness as the total on-call hours for each developer should be as similar as possible. To make life easier later we can create an intermediate array total_hours, which holds the numbers of on-call hours for every developer.
array[DEVELOPERS] of var int: total_hours = [
sum( [assignment[h]=developer | hour in HOURS ] )
| developer in DEVELOPERS
];Here we can see new syntax, a list comprehension. We iterate for every developer, and in the inner list comprehension, calculate the actual number of working hours.
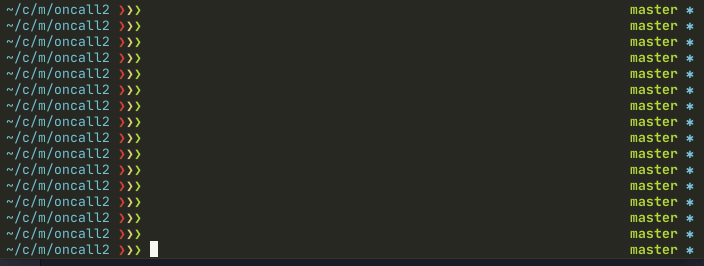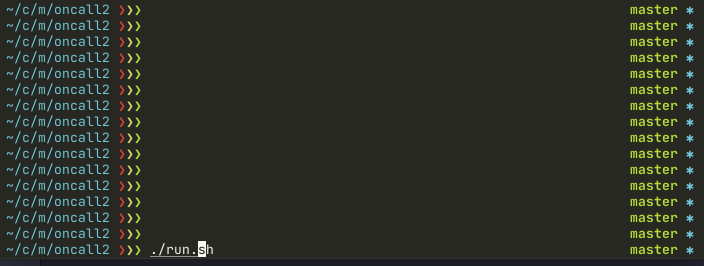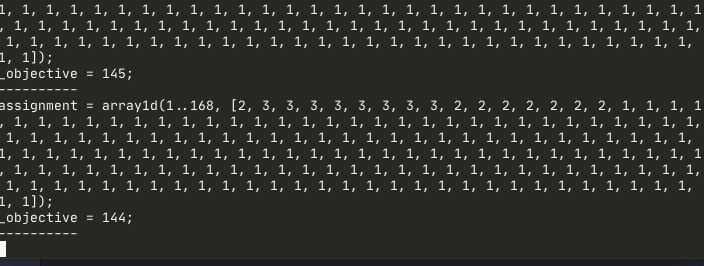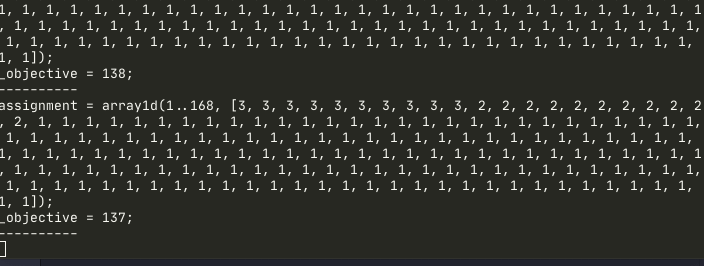
To solve for fairness, we need an expression to convert total_hours to a single number so different solutions can be compared. One option is min-max:
solve minimize max(total_hours) - min(total_hours);The minimal possible objective expression is 0 when all developers has equal total on-call hours per week. The expression is provably correct but in practice it’s pretty slow with default miniZinc optimizer, as the approach it takes is to first assign the first developer to all hours as initial solution and then try to improve it.
One option to improve performance is to tell MiniZinc to select developers randomly during search with search annotation. You can read more about this in the MiniZinc tutorial, here we’ll focus on another solution.
solve :: int_search(assignment, first_fail, indomain_random)
minimize max(total_hours) - min(total_hours);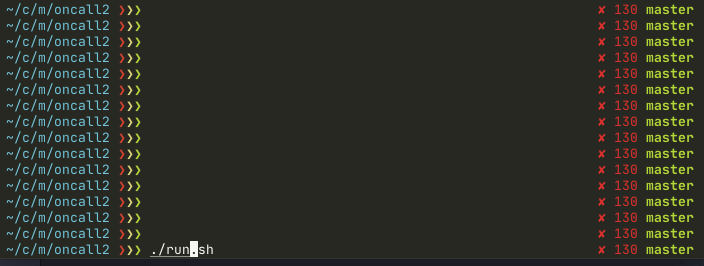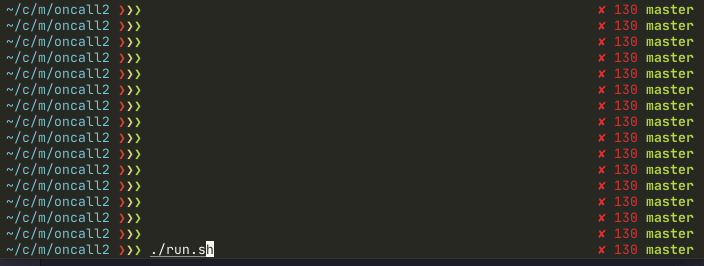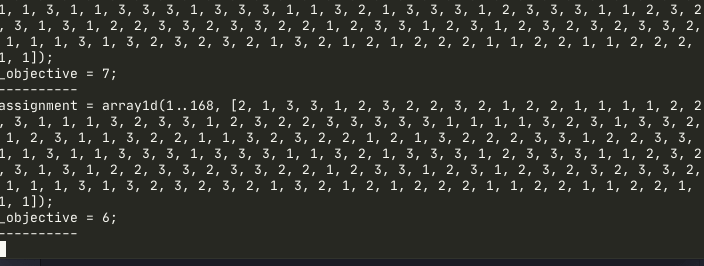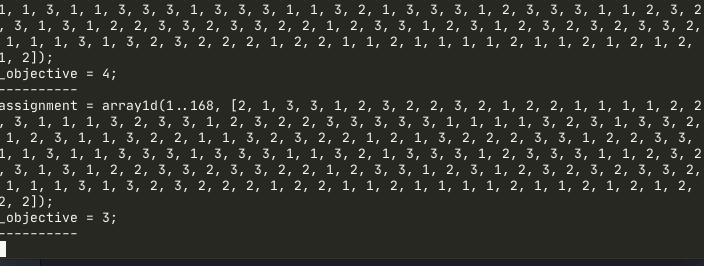
Min-max model in MiniZinc Playground or on GitHub
Even fairer fairness
The min-max objective is simple to define, but unfortunately, in some edge cases, it will not work. Minimum and maximum create boundaries and the algorithm will try to push them together as much as possible. But imagine if minimum and maximum boundaries stack at some values because some constraint, in such case min-max objective will NOT even try to optimize developers between boundaries.
Example: we have 4 developers and fair distribution of on-call hours would be 42 total hours per week for everyone [42,42,42,42], objective here equals to 0 because maximum and minimum are the same. Let’s assume we have only 1 developer in Asia timezone, so only she could cover some number of hours (let’s say 84). Now fair distribution would look like [84,28,28,28]. The model cannot decrease maximum but still assigns to all other developers equal number of hours. So far so good… but one developer is spending a week in Bahamas without internet. Now min(total_hours) equals to 0. So distributions [84,84,0,0] and [84,42,42,0] have the same objective equal to 84 but different fairness. Our objective does not represent fairness anymore.
Instead, we can use more complicated objective expression that measures the difference between all combinations of DEVELOPERS:
var int: absolute_diff = sum(developer1 in DEVELOPERS, developer2 in DEVELOPERS where developer1 > developer2)(
abs(total_hours[developer1] - total_hours[developer2])
);Again there is new syntax, but it’s slightly different list comprehension with an aggregation function on top. We iterate for all unique DEVELOPERS pairs and for each pair, calculate the absolute difference. As the last step, we sum all such differences.
Only one line left, to ask to minimize the sum of absolute differences:
solve minimize absolute_diff;Model with absolute difference objective in MiniZinc Playground or on GitHub
Working with optional variable
What happens if no developers can cover some hours? Remember that assignment is defined as array[HOURS] of var DEVELOPERS: assignment; it requires a developer for every hour, otherwise MiniZinc will report an error:
WARNING: model inconsistency detected
=====UNSATISFIABLE=====The solution is to allow some values to have a nil value. MiniZinc natively supports optional types, but I prefer to use 0 to represent optional value (because some solvers don’t have optional type; plus for future performance optimization I prefer model the problem as low-level as possible).
We need define a new range DEVELOPERS0 which includes an extra 0, and use it as a possible values of assignment array for every hour.
set of int: DEVELOPERS0 = 0..nb_developers;
array[HOURS] of var DEVELOPERS0: assignment;This actually is not enough. The objective tries to minimize the difference, and the easiest optimal result is to set all on-call hours to 0, so the objective will be 0 too. Instant optimal solution…
One way to fix this is to add a constraint: if somebody is available at some hour, then an hour should not be 0.
% calculate if developer available at specific hour
array[HOURS] of var int: is_developer_available = [
max( [working_hours[developer, hour] | developer in DEVELOPERS] )
| hour in HOURS
];
% always assign someone if there is someone available
constraint forall(hour in HOURS)(
is_developer_available[hour] = 1 -> assignment[hour] != 0
);Choosing a solver
Another complexity with discrete optimization is that you should understand what type of solver will be used before writing the model. By default, MiniZinc uses Gecode which is a smart depth-first search. It’s good enough for many models, but not for this one. Here decision tree is wide and our objective function cannot direct the search of Gecode.
Instead, from the beginning, I specifically optimized the model for Mixed Integer Programming. By optimize, I mean I tried to use boolean variables and array representation instead of sets. On the command line, we need to specify the solver to use. I use Coin-bc, a great open-sourced mixed integer programming solver included by default in MiniZinc:
minizinc oncall.mzn oncall.dzn --all-solutions --output-objective --solver Coin-bcCoin-bc returns the result faster for the model and in many cases proves optimal solution.
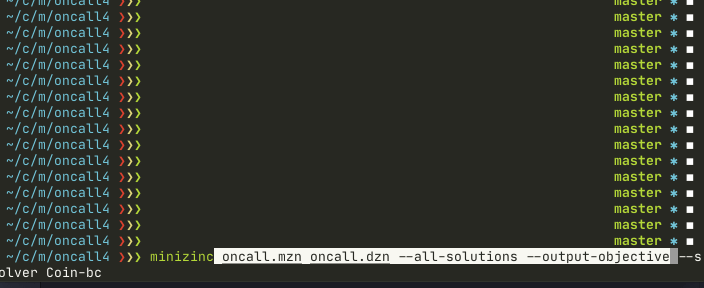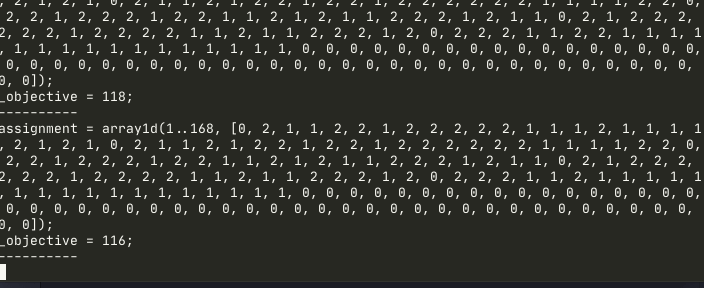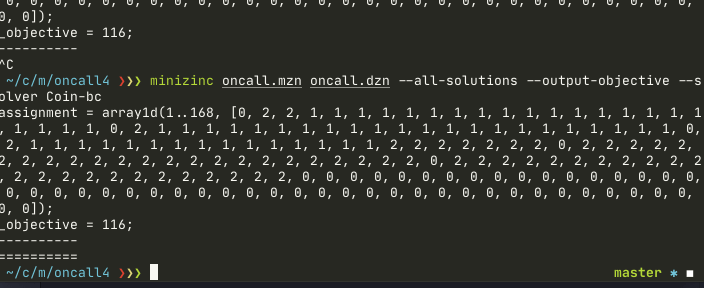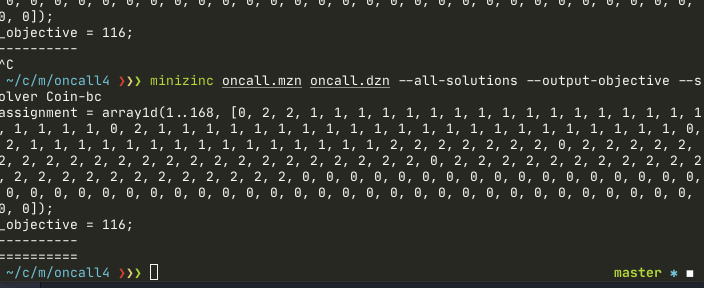
Notice how Gecode solver finds an optimal solution in a few seconds, and then still tries to improve. Coin-bc finds the solution slightly faster and proves optimality. This doesn’t mean that Coin-bc is better than Gecode – both have strengths and weaknesses. To properly explain the difference we need to dig into constraint-based algorithms(Gecode) and mixed integer programming(Coin-bc) first, and it’s too much for this article. We actually use both in production. Gecode finds first initial solution, then Coin-bc optimizes it.
Model with absolute difference objective in MiniZinc Playground (Playground only supports Gecode solver) or on GitHub
Learning materials
I found online course Discrete Optimization at the right time for me. I took time off between 2 jobs and was going to just spend a few hours to watch the course, but the leaderboard made some adjustment. I spent about 2 months full-time on solving the problems, and eventually I managed get an A on all of them. The hardest and most rewarding course in my life. Thanks to Prof. Pascal Van Hentenryck and Dr. Carleton Coffrin!
To start in this field, I’d suggest 4 online courses in order:
- Discrete Optimization from Prof. Pascal Van Hentenryck and Dr. Carleton Coffrin.
- Basic Modeling for Discrete Optimization from Prof. Peter James Stuckey and Prof. Jimmy Ho Man Lee.
- Advanced Modeling for Discrete Optimization from Prof. Peter James Stuckey and Prof. Jimmy Ho Man Lee.
- Solving Algorithms for Discrete Optimization from Prof. Peter James Stuckey and Prof. Jimmy Ho Man Lee.
Don’t forget to check out the full MiniZinc tutorial. It covers basic syntax upto advanced topics like search annotation, best modelling practices, and so on with many examples.

